차원의 저주 Curse of Dimensionality, 주성분 분석 PCA
차원의 저주 Curse of Dimensionality
"차원의 저주(Curse of Dimensionality)"는 고차원 데이터에서 발생하는 다양한 문제들을 설명하는 용어입니다. 차원의 저주가 발생하는 이유는 데이터의 차원이 증가함에 따라 데이터가 점점 희소해지고, 분석 및 모델링의 어려움이 증가하기 때문입니다. 차원의 저주가 발생하는 주요 문제와 그 해결 방법에 대해 자세히 설명하겠습니다.
차원의 저주의 주요 문제
- 데이터 희소성
- 고차원 공간에서 데이터 포인트는 매우 희소하게 분포합니다. 이는 대부분의 공간이 비어 있고, 데이터 포인트 간의 거리가 멀어지는 결과를 초래합니다.
- 예를 들어, 1차원 공간에서 10개의 데이터 포인트는 10개의 구간으로 나뉘지만, 10차원 공간에서는 10^10개의 구간으로 나뉘게 되어 데이터가 극도로 희소해집니다.
- 거리 척도 무의미
- 고차원 공간에서는 유클리드 거리 등의 거리 척도가 의미를 잃게 됩니다. 모든 데이터 포인트가 서로 거의 동일한 거리만큼 떨어져 있는 것처럼 보일 수 있습니다.
- 이는 k-최근접 이웃(k-NN) 알고리즘과 같은 거리 기반 알고리즘의 성능에 부정적인 영향을 미칩니다.
- 계산 복잡도 증가
- 차원이 증가할수록 계산량이 기하급수적으로 증가합니다. 이는 모델 학습과 예측에 더 많은 시간과 자원이 필요함을 의미합니다.
- 예를 들어, 행렬 연산에서 차원이 증가하면 행렬의 크기가 급격히 커져 계산 복잡도가 증가합니다.
- 모델 과적합
- 고차원 데이터에서는 모델이 데이터를 과도하게 학습(과적합)할 가능성이 높아집니다. 이는 모델이 훈련 데이터에 너무 특화되어 새로운 데이터에 일반화하지 못하는 문제를 초래합니다.
- 고차원 데이터에서는 모델의 복잡도가 증가하여 학습 과정에서 노이즈까지 학습할 가능성이 커집니다.
차원의 저주 해결 방법
- 차원 축소 기법
- 주성분 분석(PCA, Principal Component Analysis): 데이터의 분산을 최대한 보존하는 몇 개의 주요 성분으로 차원을 축소하는 기법입니다. 데이터의 주요 패턴을 유지하면서 차원을 줄일 수 있습니다.
- 선형 판별 분석(LDA, Linear Discriminant Analysis): 클래스 간의 분산을 최대화하고 클래스 내의 분산을 최소화하는 방향으로 차원을 축소하는 기법입니다.
- t-SNE(T-distributed Stochastic Neighbor Embedding): 고차원 데이터를 저차원으로 시각화하는 데 사용되는 기법으로, 데이터 포인트 간의 유사성을 보존합니다.
- UMAP(Uniform Manifold Approximation and Projection): 데이터의 구조를 보존하면서 저차원 공간으로 변환하는 기법입니다.
- 특징 선택(Feature Selection)
- 필터 방법(Filter Methods): 각 특징의 통계적 특성을 사용하여 중요도를 평가하고, 상위 n개의 특징을 선택하는 방법입니다. 예를 들어, 분산, 상관계수, 카이제곱 검정을 사용할 수 있습니다.
- 래퍼 방법(Wrapper Methods): 모델 성능을 기준으로 특징 조합을 평가하고 선택하는 방법입니다. 예를 들어, 전진 선택법, 후진 제거법, 단계적 선택법이 있습니다.
- 임베디드 방법(Embedded Methods): 모델 학습 과정에서 특징 선택을 수행하는 방법입니다. 예를 들어, LASSO 회귀, 릿지 회귀 등이 있습니다.
- 정규화(Regularization)
- L1 정규화(Lasso): 모델의 일부 계수를 0으로 만들어 자동으로 특징 선택을 수행합니다.
- L2 정규화(Ridge): 모든 계수를 작게 만들어 과적합을 방지합니다. L2 정규화는 특히 다중공선성 문제를 완화하는 데 유용합니다.
- 데이터 증대(Data Augmentation)
- 데이터의 양을 증가시켜 고차원 공간에서 모델이 일반화할 수 있도록 돕습니다. 예를 들어, 이미지 데이터의 경우 회전, 이동, 크기 변경 등의 기법을 사용할 수 있습니다.
결론
차원의 저주는 고차원 데이터에서 발생하는 다양한 문제들을 포괄하는 개념입니다. 이를 해결하기 위해 차원 축소, 특징 선택, 정규화 등의 방법을 사용할 수 있으며, 이러한 기법들을 통해 데이터의 차원을 효과적으로 줄이고 모델의 성능을 향상시킬 수 있습니다. 차원의 저주를 이해하고 적절한 해결 방법을 적용하는 것은 데이터 분석과 머신러닝 모델링에서 매우 중요한 부분입니다.
주성분 분석 (PCA, Principal Component Analysis)
**주성분 분석(PCA)**은 데이터의 차원을 축소하기 위해 사용되는 통계 기법입니다. 데이터의 분산을 최대한 보존하는 몇 개의 주성분(principal components)을 찾아 고차원 데이터를 저차원 공간으로 변환합니다. PCA는 특히 데이터 시각화, 잡음 제거, 데이터 압축 등에 유용합니다.
PCA의 주요 개념
- 분산 보존: PCA는 데이터의 분산을 최대한 보존하는 방향으로 주성분을 찾습니다. 분산이 크다는 것은 데이터의 중요한 변동 정보를 많이 포함하고 있음을 의미합니다.
- 직교 변환: PCA는 원래의 특징들을 새로운 직교 좌표계로 변환합니다. 새로운 좌표축은 주성분(principal components)이라 불립니다.
- 주성분: 첫 번째 주성분은 데이터의 최대 분산 방향을 나타내고, 두 번째 주성분은 첫 번째 주성분에 직교하는 방향 중에서 최대 분산을 가지는 방향을 나타냅니다. 이런 식으로 이어집니다.
PCA의 적용 과정
- 데이터 표준화: PCA를 적용하기 전에 각 특징을 표준화(평균을 0, 분산을 1로)하는 것이 일반적입니다. 이는 모든 특징이 동일한 척도로 평가될 수 있도록 합니다.
- 공분산 행렬 계산: 표준화된 데이터의 공분산 행렬을 계산합니다.
- 고유값 분해: 공분산 행렬을 고유값 분해하여 고유값(eigenvalue)과 고유벡터(eigenvector)를 구합니다.
- 주성분 선택: 고유값이 큰 순서대로 고유벡터를 정렬하고, 상위 k개의 고유벡터를 선택하여 주성분으로 사용합니다.
- 데이터 변환: 원래 데이터를 선택된 주성분으로 변환하여 새로운 저차원 데이터를 얻습니다.
PCA 적용 예시 : 4차원 데이터 2차원으로 축소
다음은 Python의 scikit-learn 라이브러리를 사용하여 PCA를 적용하는 예시입니다. 여기서는 Iris 데이터셋을 사용하여 차원을 2차원으로 축소해 보겠습니다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
# 데이터 로드
iris = load_iris()
X = iris.data
y = iris.target
# 데이터 표준화
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
# PCA 적용 (2개의 주성분)
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_std)
# 주성분 변환 후 데이터
print("원본 데이터 형태:", X.shape)
print("PCA 변환 후 데이터 형태:", X_pca.shape)
# PCA 결과 시각화
plt.figure(figsize=(8,6))
for label, color in zip(np.unique(y), ['r', 'g', 'b']):
plt.scatter(X_pca[y == label, 0], X_pca[y == label, 1], label=iris.target_names[label], c=color)
plt.xlabel('첫 번째 주성분')
plt.ylabel('두 번째 주성분')
plt.legend()
plt.title('PCA를 사용한 Iris 데이터셋의 2D 시각화')
plt.show()원본 데이터 형태: (150, 4)
PCA 변환 후 데이터 형태: (150, 2)
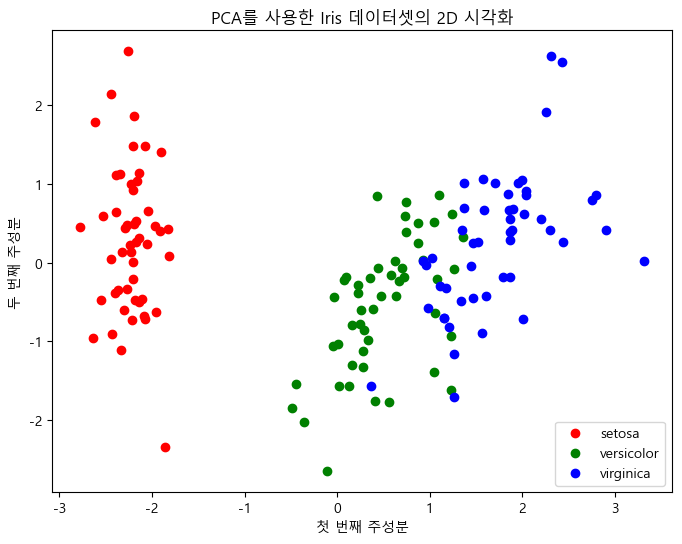
결과해석
- 데이터 표준화: PCA를 적용하기 전에 StandardScaler를 사용하여 데이터를 표준화합니다. 이는 모든 특징이 동일한 척도로 평가될 수 있도록 하는 중요한 단계입니다.
- PCA 적용: PCA(n_components=2)를 사용하여 2개의 주성분을 구합니다. 이는 원래의 4차원 데이터를 2차원으로 축소하는 과정입니다.
- 시각화: 결과적으로 얻어진 2차원 데이터를 시각화하여 각 클래스가 주성분 공간에서 어떻게 분포하는지 확인합니다.
PCA 적용 예시 : 4차원 데이터 3차원으로 축소
다음은 Python의 scikit-learn 라이브러리를 사용하여 PCA를 적용하는 예시입니다. 여기서는 Iris 데이터셋을 사용하여 차원을 3차원으로 축소해 보겠습니다. matplotlib의 Axes3D를 사용하여 3차원 시각화를 할 수 있습니다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from mpl_toolkits.mplot3d import Axes3D
# 데이터 로드
iris = load_iris()
X = iris.data
y = iris.target
# 데이터 표준화
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
# PCA 적용 (3개의 주성분)
pca = PCA(n_components=3)
X_pca = pca.fit_transform(X_std)
# 주성분 변환 후 데이터
print("원본 데이터 형태:", X.shape)
print("PCA 변환 후 데이터 형태:", X_pca.shape)
# PCA 결과 시각화 (3D)
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
for label, color, marker in zip(np.unique(y), ['r', 'g', 'b'], ['o', '^', 's']):
ax.scatter(X_pca[y == label, 0], X_pca[y == label, 1], X_pca[y == label, 2],
label=iris.target_names[label], color=color, marker=marker)
ax.set_xlabel('첫 번째 주성분')
ax.set_ylabel('두 번째 주성분')
ax.set_zlabel('세 번째 주성분')
ax.legend()
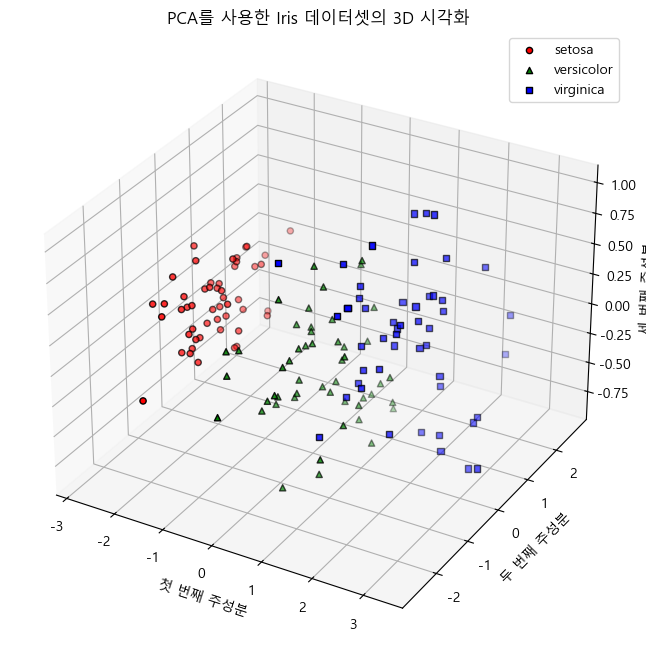
plt.title('PCA를 사용한 Iris 데이터셋의 3D 시각화')
plt.show()원본 데이터 형태: (150, 4)
PCA 변환 후 데이터 형태: (150, 3)
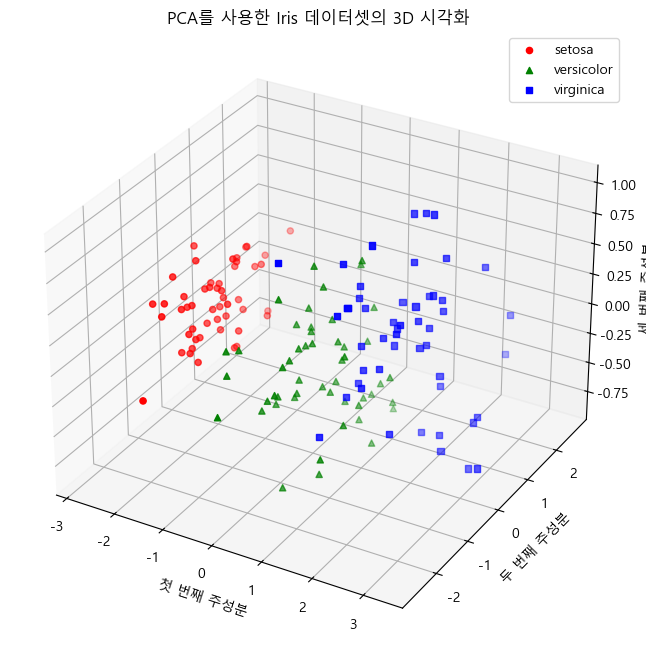
결과해석
- 데이터 로드 및 표준화: 이전과 동일하게 Iris 데이터셋을 로드하고 표준화합니다.
- PCA 적용: PCA(n_components=3)로 설정하여 3개의 주성분을 구합니다.
- 3D 시각화: mpl_toolkits.mplot3d의 Axes3D를 사용하여 3차원 그래프로 시각화합니다. 각 클래스(label)를 색상과 마커로 구분하여 표시합니다.
이렇게 하면 3차원 주성분 공간에서 데이터 포인트들이 어떻게 분포하는지 시각적으로 확인할 수 있습니다.
이 예시는 고차원 데이터를 저차원으로 축소하는 과정을 통해 데이터의 주요 패턴을 유지하면서도 시각적으로 이해하기 쉽게 만드는 방법을 보여줍니다. PCA는 차원 축소 뿐만 아니라 잡음 제거, 데이터 압축 등 다양한 분야에서도 유용하게 사용됩니다.
아이겐벡터(Eigenvector) 와 아이겐밸류(eigenvalue)
PCA(주성분 분석)에서 아이겐벡터(eigenvector)와 아이겐밸류(eigenvalue)는 매우 중요한 개념입니다. 이들은 데이터를 차원 축소하고 주요 패턴을 추출하는 데 사용됩니다. 이 두 개념을 자세히 설명하겠습니다.
아이겐벡터 (Eigenvector)
아이겐벡터는 선형 변환을 통해 그 방향이 변하지 않는 벡터를 의미합니다. PCA에서는 데이터의 공분산 행렬로부터 아이겐벡터를 구하는데, 이 아이겐벡터는 주성분의 방향을 나타냅니다. 아이겐벡터는 데이터를 설명하는 주요 축을 나타내며, 각각의 주성분(principal component)에 해당합니다.
- 특성: 아이겐벡터는 방향을 나타내며, 크기는 보통 단위 벡터로 정규화됩니다.
- 역할: PCA에서 아이겐벡터는 새로운 축을 정의하며, 이 축은 데이터의 분산을 최대한 설명하는 방향을 가리킵니다.
아이겐밸류 (Eigenvalue)
아이겐밸류는 아이겐벡터에 대응하는 값으로, 아이겐벡터의 크기 변화를 나타냅니다. PCA에서는 아이겐밸류가 주성분의 중요도를 나타내며, 각 주성분이 데이터의 총 분산에서 차지하는 비율을 의미합니다.
- 특성: 아이겐밸류는 스칼라 값이며, 각 아이겐벡터에 대해 하나씩 존재합니다.
- 역할: PCA에서 아이겐밸류는 각 주성분이 데이터의 분산을 얼마나 설명하는지를 나타냅니다. 큰 아이겐밸류를 가지는 주성분일수록 데이터의 중요한 패턴을 많이 설명합니다.
PCA에서 아이겐벡터와 아이겐밸류의 역할
PCA 과정에서 아이겐벡터와 아이겐밸류는 다음과 같은 단계에서 사용됩니다:
- 데이터 표준화: 데이터의 각 특징이 동일한 척도로 평가될 수 있도록 표준화합니다.
- 공분산 행렬 계산: 표준화된 데이터의 공분산 행렬을 계산합니다. 공분산 행렬은 데이터의 분산과 각 특징 간의 공분산을 나타냅니다.
- 아이겐벡터와 아이겐밸류 계산: 공분산 행렬을 고유값 분해하여 아이겐벡터와 아이겐밸류를 구합니다. 아이겐벡터는 공분산 행렬의 고유벡터이고, 아이겐밸류는 고유값입니다.
- 주성분 선택: 아이겐밸류가 큰 순서대로 아이겐벡터를 정렬하고, 상위 k개의 아이겐벡터를 선택하여 주성분으로 사용합니다.
- 데이터 변환: 원래 데이터를 선택된 아이겐벡터 공간으로 투영하여 차원을 축소합니다. 이 변환된 데이터는 원래 데이터의 주요 패턴을 보존합니다.
예시 코드
다음은 Python을 사용하여 PCA를 수행하고 아이겐벡터와 아이겐밸류를 구하는 예시입니다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
# 데이터 로드
iris = load_iris()
X = iris.data
# 데이터 표준화
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
# 공분산 행렬 계산
cov_matrix = np.cov(X_std.T)
# 아이겐벡터와 아이겐밸류 계산
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)
# 아이겐밸류 정렬
sorted_index = np.argsort(eigenvalues)[::-1]
sorted_eigenvalues = eigenvalues[sorted_index]
sorted_eigenvectors = eigenvectors[:, sorted_index]
# 주성분 선택 (상위 2개)
n_components = 2
selected_eigenvectors = sorted_eigenvectors[:, :n_components]
# 데이터 변환
X_pca = X_std.dot(selected_eigenvectors)
# 결과 출력
print("아이겐밸류:", sorted_eigenvalues)
print("아이겐벡터:\n", sorted_eigenvectors)
# PCA 결과 시각화
plt.figure(figsize=(8,6))
for label, color in zip(np.unique(iris.target), ['r', 'g', 'b']):
plt.scatter(X_pca[iris.target == label, 0], X_pca[iris.target == label, 1], label=iris.target_names[label], c=color)
plt.xlabel('첫 번째 주성분')
plt.ylabel('두 번째 주성분')
plt.legend()
plt.title('PCA를 사용한 Iris 데이터셋의 2D 시각화')
plt.show()아이겐밸류: [2.93808505 0.9201649 0.14774182 0.02085386]
아이겐벡터: [[ 0.52106591 -0.37741762 -0.71956635 0.26128628] [-0.26934744 -0.92329566 0.24438178 -0.12350962] [ 0.5804131 -0.02449161 0.14212637 -0.80144925] [ 0.56485654 -0.06694199 0.63427274 0.52359713]]
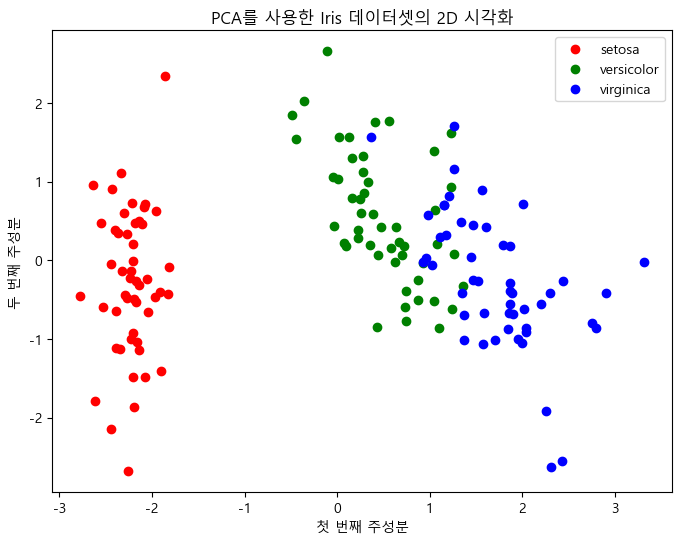
설명
- 공분산 행렬 계산: 표준화된 데이터의 공분산 행렬을 계산합니다.
- 아이겐벡터와 아이겐밸류 계산: np.linalg.eig를 사용하여 공분산 행렬의 아이겐벡터와 아이겐밸류를 계산합니다.
- 정렬 및 선택: 아이겐밸류를 내림차순으로 정렬하고, 상위 2개의 아이겐벡터를 선택합니다.
- 데이터 변환: 선택된 아이겐벡터 공간으로 데이터를 투영하여 2차원으로 변환합니다.
- 시각화: 변환된 데이터를 시각화하여 주성분 공간에서 데이터가 어떻게 분포하는지 확인합니다.
이 예시는 PCA의 기본 개념과 아이겐벡터, 아이겐밸류가 어떻게 사용되는지를 보여줍니다.
PCA의 단점
PCA(Principal Component Analysis)는 데이터 차원 축소와 주요 패턴 추출에 유용한 기법이지만, 몇 가지 단점도 있습니다. 아래에 PCA의 주요 단점을 설명하겠습니다.
PCA의 단점
- 선형성 가정
- 설명: PCA는 데이터의 주요 패턴이 선형적으로 분포한다고 가정합니다. 즉, PCA는 선형 변환을 사용하여 주성분을 찾습니다.
- 영향: 데이터가 비선형적인 구조를 가지는 경우, PCA는 이러한 구조를 효과적으로 캡처하지 못할 수 있습니다.
- 대안: 비선형 차원 축소 기법인 커널 PCA(Kernel PCA)나 t-SNE, UMAP 등을 사용할 수 있습니다.
- 해석의 어려움
- 설명: 주성분은 원래 특징의 선형 조합으로 구성되기 때문에, 해석이 직관적이지 않을 수 있습니다.
- 영향: 각 주성분이 무엇을 의미하는지, 원래 특징이 어떻게 변환되었는지 이해하기 어려울 수 있습니다.
- 대안: 주성분의 계수를 분석하여 원래 특징이 주성분에 어떻게 기여하는지 파악할 수 있습니다.
- 정보 손실
- 설명: 차원을 축소하는 과정에서 일부 정보가 손실될 수 있습니다. 특히, 주성분의 수를 적게 선택하면 더 많은 정보가 손실될 수 있습니다.
- 영향: 중요한 정보가 손실되면 모델의 성능이 저하될 수 있습니다.
- 대안: 설명된 분산 비율을 확인하여 충분한 정보를 보존하는 주성분의 수를 선택합니다.
- 스케일링의 중요성
- 설명: PCA는 각 특징의 분산에 민감합니다. 따라서, 특징이 서로 다른 스케일을 가지면 PCA 결과가 왜곡될 수 있습니다.
- 영향: 특징의 스케일 차이가 크면 특정 특징이 주성분에 과도하게 영향을 미칠 수 있습니다.
- 대안: PCA를 적용하기 전에 데이터 표준화(Standardization) 또는 정규화(Normalization)를 수행합니다.
- 데이터 중심 이동 필요
- 설명: PCA를 적용하려면 데이터를 원점(0) 중심으로 이동해야 합니다.
- 영향: 데이터의 평균을 원점으로 이동하지 않으면 PCA의 결과가 왜곡될 수 있습니다.
- 대안: PCA 적용 전에 데이터를 중앙 집중화(Centering)합니다.
- 노이즈에 민감
- 설명: PCA는 데이터의 분산을 최대화하는 방향으로 주성분을 찾기 때문에, 데이터에 존재하는 노이즈도 포함될 수 있습니다.
- 영향: 노이즈가 많은 데이터에서는 PCA가 유용하지 않을 수 있습니다.
- 대안: 노이즈를 제거하거나, 노이즈에 덜 민감한 기법을 사용합니다.
- 고차원 데이터에서의 계산 비용
- 설명: 매우 고차원 데이터에서는 공분산 행렬 계산과 고유값 분해의 계산 비용이 높을 수 있습니다.
- 영향: 대규모 데이터셋에서 PCA를 적용하는 것이 비효율적일 수 있습니다.
- 대안: 랜덤화된 PCA(Randomized PCA) 또는 인크리멘털 PCA(Incremental PCA)를 사용할 수 있습니다.
결론
PCA는 데이터 차원 축소와 주요 패턴 추출에 매우 유용한 기법이지만, 위에서 언급한 단점들을 인식하고 데이터의 특성과 목적에 맞는 적절한 대안을 고려해야 합니다. 데이터의 구조와 특성에 따라 PCA가 적절하지 않을 수 있으며, 이 경우 다른 차원 축소 기법을 사용하는 것이 바람직할 수 있습니다.
PCA를 사용해야 하는 주요 상황과 그 이유
PCA(Principal Component Analysis)는 데이터 분석과 머신러닝에서 여러 상황에서 유용하게 사용할 수 있습니다. 다음은 PCA를 사용해야 하는 주요 상황과 그 이유입니다.
PCA를 사용해야 하는 상황
- 차원 축소
- 설명: 고차원 데이터셋에서 특징의 수를 줄여 모델의 복잡성을 낮추고 계산 비용을 줄입니다.
- 이유: 차원을 축소하면 모델의 학습과 예측 속도가 빨라지고, 과적합(overfitting)을 방지할 수 있습니다.
- 적용: 데이터의 분산을 최대한 보존하면서 차원을 줄일 때 PCA를 사용합니다.
- 데이터 시각화
- 설명: 고차원 데이터를 2차원 또는 3차원으로 변환하여 시각적으로 이해할 수 있도록 합니다.
- 이유: 주성분으로 변환된 데이터는 중요한 패턴과 그룹을 시각적으로 쉽게 파악할 수 있게 합니다.
- 적용: 특히, 탐색적 데이터 분석(EDA) 단계에서 데이터의 구조와 패턴을 시각화할 때 유용합니다.
- 노이즈 제거
- 설명: 데이터의 주요 변동을 설명하지 못하는 작은 주성분을 제거하여 노이즈를 감소시킵니다.
- 이유: 노이즈가 제거된 데이터는 모델의 성능을 향상시키고, 더 명확한 패턴을 발견하는 데 도움이 됩니다.
- 적용: 데이터의 주성분을 분석하여 노이즈가 대부분 포함된 주성분을 제거합니다.
- 특징 선택 및 생성
- 설명: 중요한 특징을 선택하거나 새로운 주성분을 생성하여 특징 공간을 재구성합니다.
- 이유: 특징 간의 상관관계를 줄이고, 모델의 성능을 개선할 수 있습니다.
- 적용: 상관관계가 높은 특징들이 많은 데이터셋에서 PCA를 사용하여 독립적인 주성분을 생성합니다.
- 데이터 압축
- 설명: 데이터의 크기를 줄여 저장 공간을 절약하고, 전송 속도를 향상시킵니다.
- 이유: 중요한 정보를 최대한 보존하면서 데이터의 차원을 줄여 데이터 압축 효과를 얻을 수 있습니다.
- 적용: 고차원 데이터를 저차원으로 압축하여 데이터 저장 및 전송 효율성을 높입니다.
- 다중공선성 문제 해결
- 설명: 다중공선성이 있는 데이터셋에서 독립적인 주성분을 사용하여 모델을 구축합니다.
- 이유: 다중공선성은 회귀 분석과 같은 모델에서 문제를 일으킬 수 있으므로, 이를 해결하기 위해 PCA를 사용합니다.
- 적용: 다중공선성이 존재하는 회귀 분석에서 독립적인 주성분을 예측 변수로 사용합니다.
PCA 적용 예시
예시 1: 차원 축소와 시각화
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
# 2개의 주성분 사용
pca_2d = PCA(n_components=2)
X_pca_2d = pca_2d.fit_transform(X_std)
# 3개의 주성분 사용
pca_3d = PCA(n_components=3)
X_pca_3d = pca_3d.fit_transform(X_std)
# 2D 시각화
plt.figure(figsize=(8, 6))
for label, color, marker in zip(np.unique(y), ['r', 'g', 'b'], ['o', '^', 's']):
plt.scatter(X_pca_2d[y == label, 0], X_pca_2d[y == label, 1], label=iris.target_names[label], color=color, marker=marker, edgecolor='k')
plt.xlabel('첫 번째 주성분')
plt.ylabel('두 번째 주성분')
plt.legend()
plt.title('PCA를 사용한 Iris 데이터셋의 2D 시각화')
plt.show()
# 3D 시각화
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
for label, color, marker in zip(np.unique(y), ['r', 'g', 'b'], ['o', '^', 's']):
ax.scatter(X_pca_3d[y == label, 0], X_pca_3d[y == label, 1], X_pca_3d[y == label, 2],
label=iris.target_names[label], color=color, marker=marker, edgecolor='k')
ax.set_xlabel('첫 번째 주성분')
ax.set_ylabel('두 번째 주성분')
ax.set_zlabel('세 번째 주성분')
ax.legend()
plt.title('PCA를 사용한 Iris 데이터셋의 3D 시각화')
plt.show()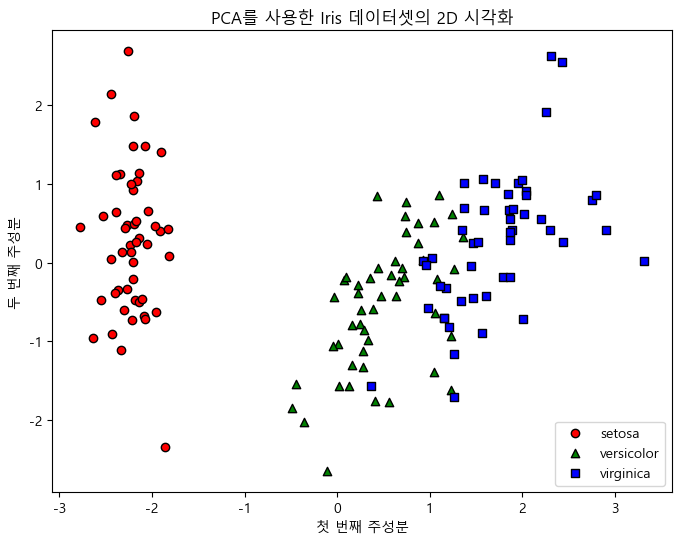
예시 2: 노이즈 제거
from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
plt.rcParams['font.family'] ='Malgun Gothic'
plt.rcParams['axes.unicode_minus'] =False
# 데이터 로드
digits = load_digits()
X = digits.data
# PCA 적용 (30개의 주성분)
pca = PCA(n_components=30)
X_pca = pca.fit_transform(X)
X_inverse = pca.inverse_transform(X_pca)
# 원본 이미지와 PCA 복원 이미지 비교
fig, axes = plt.subplots(1, 2, figsize=(8, 4), subplot_kw={'xticks':[], 'yticks':[]}, gridspec_kw=dict(hspace=0.3, wspace=0.05))
ax = axes.ravel()
ax[0].imshow(digits.data[0].reshape(8, 8), cmap='gray')
ax[0].set_title('Original Image')
ax[1].imshow(X_inverse[0].reshape(8, 8), cmap='gray')
ax[1].set_title('PCA Compressed Image')
plt.show()
결론
PCA는 차원 축소, 시각화, 노이즈 제거, 특징 선택, 데이터 압축, 다중공선성 문제 해결 등 다양한 상황에서 유용하게 사용됩니다. 데이터의 특성과 분석 목적에 따라 PCA를 적절히 활용하면 데이터 분석과 머신러닝 모델의 성능을 크게 향상시킬 수 있습니다.