Table of Contents
Convex의 정의
Convex는 볼록하다는 것을 의미한다.
함수의 Convexity
Convex 함수는 볼록 함수라고 하며, 이름 그대로 볼록한 함수를 의미한다. 아래로 볼록한 것 Convex라 하며, 위로 볼록한 함수는 Concave라 한다.

우리가 가장 잘 아는 Convex 함수는 위와 같은 이차함수이다. 이름 그대로 아래로 볼록한 모양의 그래프를 갖는다.
그렇다면 이러한 Convex 함수를 수학적으로 판단하는 방법은 무엇일까? 함수 위의 임의의 두 점을 연결하는 선을 그래프에 그었을 때, 그 선이 아래 그림과 같이 함수 그래프의 위쪽만을 지나가면 이 함수는 convex 한 함수이다.

반면, 함수위의 임의의 두 점을 연결하는 선이 함수의 아래를 지난다면 이것은 non-convex 함수이다.

Convex 함수의 판별
함수 위의 임의의 두 점 𝑥,𝑦와 [0,1] 사이의 값 𝑡에 대해 다음이 식이 항상 성립하면 이 함수는 Convex 하다고 말할 수 있다.

Convexity와 딥러닝
딥러닝은 매우 복잡한 다변수 함수의 최적해를 경사 하강법을 통해 찾는다.
경사 하강법을 사용할 때, convex 함수와 non-convex 함수에서 탐색한 해는 큰 차이를 갖는다.

위와 같은 convex 함수의 경우, 우리가 딥러닝에서 경사 하강법을 통해 찾는 최저점이 단 하나 존재한다.
이 점을 전역 최적해Global Minimum이라고 한다.
Convex 함수에 대한 경사 하강법은 하나의 최고의 해로 수렴한다. 그러나 non-convex 함수에서는 그렇지 않다.

non-convex 함수는 무한히 넓은 함수 공간에서 여러 곳의 지역 최저점Local minima을 갖는다.
위 함수에서 이로 인하여, 경사 하강법을 시작하는 위치에 따라 서로 다른 최저점을 향해 결과가 수렴하게 된다. 예를 들어, 위 함수에서 1.5에서 경사 하강법을 시행하면 0.3 부근의 지역 최저점으로 수렴할 것이다. 그러나 2.5 부근에서 경사 하강법을 시행했다면, 조금 더 나은 결과를 갖는 5 부근의 지역 최저점으로 수렴할 것이다.
non-convex 함수의 문제는 우리가 어디가 전역 최적해인지를 알 수가 없다는 것이다. 이로 인해 non-convex 한 문제를 딥러닝으로 해결하려고 하면 학습이 잘 되지 않고 좋지 않은 지역 최저점에 갇히는 등의 문제가 발생한다.
머신러닝(ML)과 딥러닝(DL)에서 Convex 함수가 중요한 역할을 하기는 하지만, "무조건 좋은 함수"라고 말하기에는 여러 가지 고려해야 할 사항이 있다.
Convex 함수의 특성
Convex 함수는 어떤 함수 f가 주어진 두 점 x와 y에 대해 다음과 같은 조건을 만족할 때 Convex라고 한다:
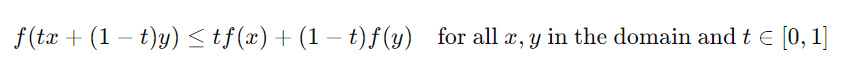
이러한 성질을 가진 함수는 그래프가 "볼록"한 형태를 가지며, 이는 두 점을 연결하는 선분이 함수의 그래프 위에 있음을 의미한다.
머신러닝과 딥러닝에서의 Convex 함수
- 머신러닝에서의 Convex 최적화: 많은 머신러닝 알고리즘, 특히 선형 회귀(linear regression)나 로지스틱 회귀(logistic regression)와 같은 모델은 비용 함수(cost function) 또는 손실 함수(loss function)가 Convex 형태인 경우가 많다. 이런 경우에는 전역 최솟값(global minimum)을 보장하며, 이 최솟값을 효과적으로 찾을 수 있는 알고리즘이 잘 개발되어 있다(예: 경사 하강법).
- 딥러닝에서의 비Convex 함수: 대부분의 딥러닝 모델, 특히 심층 신경망은 비Convex 손실 함수를 가진다. 이는 함수의 곡면에 여러 개의 지역 최소값(local minima)과 안장점(saddle points)이 존재함을 의미한다. 이 경우, 전역 최소값을 찾는 것은 매우 어렵고, 때로는 불가능할 수도 있다. 그러나 실제로 딥러닝 모델에서는 지역 최소값이 전역 최소값과 유사한 성능을 내는 경우가 많아, 실제 응용에는 큰 문제가 되지 않을 수 있다.
Convex 함수가 "무조건 좋은"가?
- 장점: Convex 함수의 경우 최적화가 상대적으로 쉽고, 수학적으로 분석하기 용이하다. Convex 최적화 문제는 전역 최소값을 찾을 수 있다는 강력한 보장을 제공한다.
- 단점: 현실의 많은 문제, 특히 이미지나 음성 인식과 같은 복잡한 패턴을 인식하는 딥러닝 문제는 Convex 함수로 모델링하기 어렵다. 이러한 문제들은 본질적으로 비Convex 성질을 가지고 있으며, 이 경우 비Convex 최적화 기법을 사용해야 한다.
결론적으로, Convex 함수가 특정 문제에 대해 좋은 솔루션을 제공할 수는 있지만, 모든 머신러닝 또는 딥러닝 문제에 대한 "무조건 좋은 함수"는 아니다. 문제의 복잡성과 특성에 따라 적절한 함수와 최적화 기법을 선택하는 것이 중요하다.
손실 함수의 선택은 최적화 문제가 Convex 혹은 Non-Convex가 될 수 있다
손실 함수의 선택에 따라 해당 최적화 문제가 Convex 혹은 Non-Convex가 될 수 있다. 손실 함수는 모델이 예측한 결과와 실제 데이터 간의 차이를 수치적으로 나타내는 함수로, 모델 학습의 목표는 이 손실 함수의 값을 최소화하는 것이다. 손실 함수의 형태와 모델 파라미터의 특성에 따라 최적화 문제의 본질이 결정된다.
Convex 손실 함수
Convex 손실 함수는 주로 간단한 머신러닝 모델에서 발견된다. 이런 함수들은 전역 최소값을 보장하는 속성을 가지고 있어 최적화가 비교적 쉽다. 예를 들어:
- 선형 회귀에서 사용되는 **평균 제곱 오차(Mean Squared Error, MSE)**는 파라미터에 대해 Convex 함수다.
- 로지스틱 회귀에서 사용되는 **로지스틱 손실 함수(Logistic Loss)**도 모델 파라미터에 대해 Convex다.
이러한 손실 함수들은 각각의 문제에 대해 단일한 최소값을 가진다. 모델 파라미터의 공간에서 어느 지점에서 시작하더라도, 경사 하강법과 같은 최적화 알고리즘을 사용하면 전역 최소값으로 수렴할 수 있다.
Non-Convex 손실 함수
대부분의 딥러닝 모델, 특히 심층 신경망에서는 Non-Convex 손실 함수가 사용된다. 이러한 손실 함수는 다음과 같은 특징을 가진다:
- **여러 개의 지역 최소값(Local Minima)**과 **안장점(Saddle Points)**을 가질 수 있다.
- **교차 엔트로피(Cross-Entropy Loss)**는 분류 문제에서 널리 사용되며, 딥러닝 모델에서는 일반적으로 Non-Convex 속성을 가진다.
Non-Convex 손실 함수는 최적화가 더 복잡하며, 초기 파라미터의 선택이나 최적화 알고리즘의 선택에 따라 결과가 크게 달라질 수 있다. 이 경우, 경사 하강법을 사용하여 최적화를 수행할 때, 적절한 학습 속도, 모멘텀, 초기화 방법 등을 조심스럽게 선택해야 한다.
결론
따라서, 손실 함수의 선택은 모델의 학습 방식과 최적화의 복잡성에 큰 영향을 미친다. Convex 손실 함수는 최적화가 비교적 간단하지만, 모델의 표현력이 제한될 수 있다. 반면, Non-Convex 손실 함수는 최적화가 더 도전적일 수 있지만, 보다 복잡한 데이터 패턴을 모델링 할 수 있어 딥러닝에서 널리 사용된다.
Reference: https://skyil.tistory.com/33
'DeepLearning' 카테고리의 다른 글
| ReLU (Rectified Linear Unit) (0) | 2024.06.27 |
|---|---|
| 인공신경망은 MLE 기계다! (0) | 2024.06.27 |
| DNN CNN RNN GAN ? (0) | 2024.06.26 |
| 텐서 Tensor (0) | 2024.06.19 |
| [패스트캠퍼스] Upstage AI Lab 3기 학습 블로그_ ML 프로젝트 기본 이론 : Deep Learning & Pytorch 다중 퍼셉트론(Multi-Layer Perceptron, MLP) (0) | 2024.06.19 |
- Total
- Today
- Yesterday
- cnn
- LLM
- Array
- speaking
- 파이썬
- classification
- t5
- Lora
- #패스트캠퍼스 #UpstageAILab #Upstage #부트캠프 #AI #데이터분석 #데이터사이언스 #무료교육 #국비지원 #국비지원취업 #데이터분석취업 등
- #패스트캠퍼스 #패스트캠퍼스ai부트캠프 #업스테이지패스트캠퍼스 #upstageailab#국비지원 #패스트캠퍼스업스테이지에이아이랩#패스트캠퍼스업스테이지부트캠프
- 손실함수
- clustering
- LIST
- 해시
- Github
- nlp
- Python
- 코딩테스트
- 티스토리챌린지
- English
- #패스트캠퍼스 #패스트캠퍼스AI부트캠프 #업스테이지패스트캠퍼스 #UpstageAILab#국비지원 #패스트캠퍼스업스테이지에이아이랩#패스트캠퍼스업스테이지부트캠프
- 리스트
- git
- recursion #재귀 #자료구조 # 알고리즘
- 오블완
- Numpy
- Transformer
- RAG
- Hugging Face
- PEFT
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |

