Table of Contents
문제
https://leetcode.com/problems/linked-list-cycle/
- Linked List Cycle
Easy
152951340Add to ListShare
Given head, the head of a linked list, determine if the linked list has a cycle in it.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to. Note that pos is not passed as a parameter.
Return true if there is a cycle in the linked list. Otherwise, return false.
Example 1:
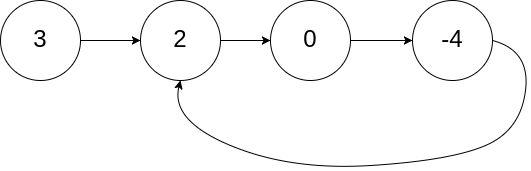
Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).Example 2:
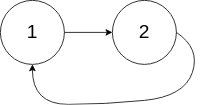
Input: head = [1,2], pos = 0
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 0th node.Example 3:

Input: head = [1], pos = -1
Output: false
Explanation: There is no cycle in the linked list.Constraints:
- The number of the nodes in the list is in the range [0, 104].
- -105 <= Node.val <= 105
- pos is -1 or a valid index in the linked-list.
풀이방법
이 문제는 LeetCode에서 주어진 단방향 연결 리스트가 사이클을 포함하고 있는지 확인하는 것입니다. 사이클이란, 연결 리스트의 한 노드에서 시작하여 `next` 포인터를 따라가다 보면 다시 그 노드로 돌아올 수 있는 경우를 말합니다.
여기서 문제에서 주어진 `pos`는 리스트의 꼬리 노드가 연결된 노드의 인덱스를 나타냅니다. 예를 들어, 리스트의 마지막 노드가 리스트의 중간에 있는 어떤 노드로 다시 연결된다면, 그 인덱스를 `pos`로 표현합니다. 하지만 이 문제를 해결할 때 `pos` 값은 함수의 매개변수로 주어지지 않습니다. 우리는 오직 연결 리스트의 `head` 노드만 주어지며, 이 `head` 노드를 기반으로 사이클 여부를 판단해야 합니다.
문제 해결 방법
Floyd의 토끼와 거북이 알고리즘을 사용하여 이 문제를 해결할 수 있습니다. 이 알고리즘은 두 개의 포인터를 사용하는데, 하나는 한 단계씩 이동하고(`slow`), 다른 하나는 두 단계씩 이동합니다(`fast`). 만약 리스트에 사이클이 있다면, 두 포인터는 결국 만납니다.
코드 구현
아래는 Floyd의 토끼와 거북이 알고리즘을 사용하여 사이클을 탐지하는 파이썬 코드입니다:
# 단방향 연결 리스트의 노드 정의
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
# 사이클을 확인하는 솔루션 클래스 정의
class Solution:
def hasCycle(self, head: Optional[ListNode]) -> bool:
# 리스트가 비어 있거나 노드가 하나만 있는 경우 사이클이 있을 수 없다
if not head or not head.next:
return False
# 두 개의 포인터 초기화
slow = head
fast = head
# 리스트를 순회
while fast and fast.next:
slow = slow.next # 느린 포인터는 한 단계씩 이동
fast = fast.next.next # 빠른 포인터는 두 단계씩 이동
# 느린 포인터와 빠른 포인터가 만나면 사이클이 존재함을 의미
if slow == fast:
return True
# 여기까지 오면 사이클이 없음을 의미
return False코드 설명
- **기본 조건 확인**: 리스트가 비어 있거나 노드가 하나만 있는 경우(`head`가 `None`이거나 `head.next`가 `None`), 사이클이 있을 수 없으므로 `False`를 반환합니다.
- **포인터 초기화**: 두 개의 포인터(`slow`와 `fast`)를 초기화합니다. 두 포인터 모두 `head`에서 시작합니다.
- **리스트 순회**: `fast` 포인터나 `fast.next`가 `None`이 될 때까지 순회합니다.
- `slow` 포인터는 한 단계씩 이동합니다.
- `fast` 포인터는 두 단계씩 이동합니다.
- **사이클 탐지**: `slow` 포인터와 `fast` 포인터가 만나면 사이클이 존재함을 의미하므로 `True`를 반환합니다.
- **사이클 없음**: 포인터들이 만나지 않고 순회가 종료되면 사이클이 없음을 의미하므로 `False`를 반환합니다.
이 알고리즘은 시간 복잡도 O(n)과 공간 복잡도 O(1)로 매우 효율적입니다.
왜 세 단계씩 이동하지 않는가?
Floyd의 토끼와 거북이 알고리즘에서 두 포인터를 사용하는 이유는 서로 다른 속도로 이동함으로써 사이클을 빠르게 탐지하기 위함입니다. 하나는 한 번에 한 단계씩(slow), 다른 하나는 두 단계씩(fast) 이동합니다. 이 접근법이 사이클 탐지에 매우 효과적입니다.
왜 세 단계씩 이동하는 포인터를 사용하지 않는지에 대한 이유는 다음과 같습니다:
- 효율적인 충돌 탐지:
- 한 포인터가 한 단계씩(
slow) 이동하고, 다른 포인터가 두 단계씩(fast) 이동하면, 사이클이 존재할 경우 두 포인터가 언젠가 반드시 만나게 됩니다. 이 방법은 최소한의 이동으로 빠르게 충돌을 탐지할 수 있습니다. - 예를 들어,
slow가 한 번에 한 단계씩 이동하고,fast가 한 번에 두 단계씩 이동하면,fast는slow를 따라잡는 데 필요한 시간 내에 사이클 내에서slow를 만날 수 있습니다.
- 한 포인터가 한 단계씩(
- 복잡성 증가:
- 만약 세 단계씩 이동하는 포인터를 사용하게 되면, 포인터들이 서로 만나지 못하는 경우가 발생할 수 있습니다. 이렇게 되면 충돌 탐지가 어려워질 수 있습니다.
- 예를 들어, 리스트의 길이와 사이클의 길이에 따라 세 단계씩 이동하는
fast포인터가slow포인터를 건너뛰는 상황이 발생할 수 있습니다.
- 알고리즘의 보편성:
- Floyd의 토끼와 거북이 알고리즘은 이미 수학적으로 증명된 효율적인 알고리즘입니다. 한 단계와 두 단계씩 이동하는 방법이 가장 단순하면서도 강력한 사이클 탐지 방법임이 증명되었습니다.
이 코드는 효율적이고 검증된 방법으로 사이클을 탐지합니다. 세 단계씩 이동하는 포인터를 사용하면 알고리즘의 신뢰성과 효율성이 떨어질 수 있기 때문에 사용하지 않습니다.
예시적용하여 상세하게 풀이
예를 들어, 다음과 같은 연결 리스트가 있다고 가정해봅시다:
- 리스트: 3 -> 2 -> 0 -> -4
- 사이클: tail이 두 번째 노드(값이 2)로 연결
이 예시를 코드에 적용하면 어떻게 사이클을 탐지하는지 한 줄씩 살펴보겠습니다. 먼저, 연결 리스트를 설정하는 코드를 작성하겠습니다.
설정 코드:
# 단방향 연결 리스트의 노드 정의
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
# 연결 리스트 생성 및 사이클 설정
head = ListNode(3)
second = ListNode(2)
third = ListNode(0)
fourth = ListNode(-4)
head.next = second
second.next = third
third.next = fourth
fourth.next = second # 사이클 설정, tail이 두 번째 노드로 연결Floyd의 토끼와 거북이 알고리즘을 사용한 사이클 탐지 코드:
class Solution:
def hasCycle(self, head: Optional[ListNode]) -> bool:
if not head or not head.next:
return False
slow = head
fast = head
while fast and fast.next:
slow = slow.next
fast = fast.next.next
# 결과값을 출력
print(f"slow: {slow.val}, fast: {fast.val}")
if slow == fast:
print("Cycle detected")
return True
print("No cycle detected")
return False
# 실행
solution = Solution()
solution.hasCycle(head)실행 결과:
코드를 실행하면 다음과 같은 출력이 나타납니다:
초기화 단계:
slow = head(값: 3)fast = head(값: 3)
첫 번째 반복:
slow는 한 단계 이동:slow = slow.next(값: 2)fast는 두 단계 이동:fast = fast.next.next(값: 0)- 출력:
slow: 2, fast: 0
두 번째 반복:
slow는 한 단계 이동:slow = slow.next(값: 0)fast는 두 단계 이동:fast = fast.next.next(값: 2)- 출력:
slow: 0, fast: 2
세 번째 반복:
slow는 한 단계 이동:slow = slow.next(값: -4)fast는 두 단계 이동:fast = fast.next.next(값: -4)- 출력:
slow: -4, fast: -4
여기서
slow와fast가 같은 노드를 가리키고 있으므로 사이클이 존재한다고 판단합니다.- 출력:
Cycle detected
결론:
이 예시에서는 세 번째 반복에서 slow와 fast가 만납니다. 이는 리스트에 사이클이 있음을 의미합니다. 따라서 최종 출력은 "Cycle detected"가 됩니다.
풀이방법 영어
This problem from LeetCode asks you to determine if a given singly linked list contains a cycle. A cycle occurs if any node in the list points back to a previous node, forming a loop. The problem refers to pos, which is the index of the node where the cycle begins, but this pos value is not provided as an input to your function. You only get the head node of the linked list, and you need to detect if a cycle exists based on this head.
Solution Approach
We can use Floyd's Tortoise and Hare algorithm, which employs two pointers moving at different speeds. The key idea is that if there's a cycle, the fast pointer will eventually catch up to the slow pointer within the cycle.
Implementation
Here's how you can implement this algorithm in Python:
# Definition for singly-linked list.
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
class Solution:
def hasCycle(self, head: Optional[ListNode]) -> bool:
# If the list is empty or has only one node, it cannot have a cycle
if not head or not head.next:
return False
# Initialize two pointers
slow = head
fast = head
# Traverse the list
while fast and fast.next:
slow = slow.next # Move slow pointer by 1 step
fast = fast.next.next # Move fast pointer by 2 steps
# If the slow pointer and fast pointer meet, there is a cycle
if slow == fast:
return True
# If we reach here, there is no cycle
return FalseExplanation of the Code
- Base Case Check: If the list is empty (
headisNone) or has only one node (head.nextisNone), there cannot be a cycle, so we returnFalse. - Pointer Initialization: Two pointers,
slowandfast, are initialized at the head of the list. - Traversal Loop: Continue traversing the list until
fastorfast.nextisNone.- Move the
slowpointer one step forward. - Move the
fastpointer two steps forward.
- Move the
- Cycle Detection: If the
slowpointer meets thefastpointer, a cycle exists, so we returnTrue. - No Cycle: If the loop terminates without the pointers meeting, return
False.
Why Use One Step and Two Steps?
- Efficient Detection: Using one-step (
slow) and two-step (fast) pointers ensures that if there is a cycle, the fast pointer will catch up to the slow pointer within a limited number of steps. - Three Steps Issue: If the fast pointer moved three steps at a time, it could skip over the slow pointer entirely in some cases, making cycle detection unreliable. The one-step and two-step approach is mathematically proven to work efficiently for this purpose.
This method provides an efficient way to detect cycles with O(n) time complexity and O(1) space complexity, making it an optimal solution for this problem.
In Floyd's Tortoise and Hare algorithm, we use two pointers with different step sizes (one step and two steps) to detect a cycle efficiently. Here's why we use these step sizes and not three steps:
Why One Step and Two Steps?
- Efficient Cycle Detection:
- With one pointer moving one step at a time (
slow) and another moving two steps at a time (fast), if there is a cycle, the fast pointer will eventually catch up to the slow pointer. This happens because the fast pointer closes the gap by one step each iteration. - For example, if the slow pointer moves to position
i, the fast pointer moves to positioni + kwherekis the number of iterations. Eventually, they will meet within the cycle.
- With one pointer moving one step at a time (
- Complexity Increase with Three Steps:
- Using a three-step pointer (
fast) could cause it to skip over the slow pointer in some cases, making the cycle detection less reliable. - The fast pointer moving three steps at a time might miss the exact point where it would meet the slow pointer, especially if the cycle length is not a multiple of three.
- Using a three-step pointer (
- Proven Algorithm:
- Floyd's algorithm with one-step and two-step pointers is mathematically proven to be efficient for cycle detection. It ensures that the fast pointer will either reach the end of the list (no cycle) or meet the slow pointer within the cycle.
Implementation:
Here's the implementation of Floyd's Tortoise and Hare algorithm in Python:
# Definition for singly-linked list.
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
class Solution:
def hasCycle(self, head: Optional[ListNode]) -> bool:
# If the list is empty or has only one node, it cannot have a cycle
if not head or not head.next:
return False
# Initialize two pointers
slow = head
fast = head
# Traverse the list
while fast and fast.next:
slow = slow.next # Move slow pointer by 1 step
fast = fast.next.next # Move fast pointer by 2 steps
# If the slow pointer and fast pointer meet, there is a cycle
if slow == fast:
return True
# If we reach here, there is no cycle
return FalseExplanation of the Code:
- Base Case Check: If the list is empty (
headisNone) or has only one node (head.nextisNone), there cannot be a cycle, so returnFalse. - Pointer Initialization: Two pointers,
slowandfast, are initialized at the head of the list. - Traversal Loop: Continue traversing the list until
fastorfast.nextisNone.- Move the
slowpointer one step forward. - Move the
fastpointer two steps forward.
- Move the
- Cycle Detection: If the
slowpointer meets thefastpointer, a cycle exists, so returnTrue. - No Cycle: If the loop terminates without the pointers meeting, return
False.
This approach ensures efficient cycle detection with a time complexity of O(n) and a space complexity of O(1). Using three steps for the fast pointer could complicate the detection process and reduce reliability, which is why it is not used in this algorithm.
'코딩테스트' 카테고리의 다른 글
| 코딩테스트 푸는 방법 코테 풀기 팁 (0) | 2024.05.21 |
|---|---|
| [파이썬] 스택/큐 > 다리를 지나는 트럭 (0) | 2024.05.21 |
| DFS(Depth-First Search) vs BFS(Breadth-First Search) (0) | 2024.05.20 |
| 리스트 내의 최솟값과 최대값 (1) | 2024.04.28 |
| 리스트 내의 특정 요소들을 리스트에 담지 않고 출력하려면? (0) | 2024.04.28 |
- Total
- Today
- Yesterday
- recursion #재귀 #자료구조 # 알고리즘
- Array
- 오블완
- #패스트캠퍼스 #패스트캠퍼스ai부트캠프 #업스테이지패스트캠퍼스 #upstageailab#국비지원 #패스트캠퍼스업스테이지에이아이랩#패스트캠퍼스업스테이지부트캠프
- clustering
- classification
- Hugging Face
- #패스트캠퍼스 #UpstageAILab #Upstage #부트캠프 #AI #데이터분석 #데이터사이언스 #무료교육 #국비지원 #국비지원취업 #데이터분석취업 등
- 손실함수
- English
- Transformer
- Github
- Numpy
- t5
- git
- 코딩테스트
- Python
- #패스트캠퍼스 #패스트캠퍼스AI부트캠프 #업스테이지패스트캠퍼스 #UpstageAILab#국비지원 #패스트캠퍼스업스테이지에이아이랩#패스트캠퍼스업스테이지부트캠프
- cnn
- 파이썬
- PEFT
- Lora
- LLM
- nlp
- LIST
- 리스트
- 해시
- speaking
- RAG
- 티스토리챌린지
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |

