[파이썬] 스택/큐 > 주식가격

코딩테스트

[파이썬] 스택/큐 > 주식가격

꼬꼬마코더 2024. 5. 23. 20:34

728x90

큐로 문제풀기

https://school.programmers.co.kr/learn/courses/30/lessons/42584

이번 문제 역시 큐를 활용하면 되는 문제입니다. 큐를 만들어주고 while문을 만들고 그 안에 초기 비교변수를 popleft 해줍니다. 그 다음 다른 값들과 비교변수의 크기를 비교하면 됩니다.

from collections import deque
def solution(prices):
    answer = []
    prices = deque(prices)
    
    while prices:
        price = prices.popleft()
        time = 0
        
        for nextprice in prices:
            time += 1
            if price > nextprice:
                break
        answer.append(time)
    return answer

통과는 했는데 정확성도 낮고 효율성이 좋지 않네요. 제 능력으론 여기까지 입니다. chatGPT 4o에게 더 나은 방법이 있는지 물어보겠습니다.

스택으로 문제풀기

현재 코드는 정확하게 동작하지만, 효율성을 높일 수 있는 몇 가지 방법이 있습니다. deque를 사용하여 popleft를 효율적으로 수행하고 있지만, for 루프 내에서 남은 모든 가격을 반복하는 것이 비효율적일 수 있습니다. 대신, 이중 반복문을 사용하여 각 가격에 대해 한 번만 계산하는 방법으로 개선할 수 있습니다.
다음은 더 효율적이고 정확한 코드입니다:

def solution(prices):
    answer = [0] * len(prices)
    stack = []
    
    for i, price in enumerate(prices):
        # 스택이 비어 있지 않고 현재 가격이 스택의 마지막 가격보다 작으면
        while stack and price < prices[stack[-1]]:
            j = stack.pop()
            answer[j] = i - j
        stack.append(i)
    
    # 스택에 남아 있는 인덱스들에 대해 가격이 떨어지지 않았던 시간 계산
    while stack:
        j = stack.pop()
        answer[j] = len(prices) - 1 - j
    
    return answer

# 테스트
prices = [1, 2, 3, 2, 3]
print(solution(prices))  # 출력: [4, 3, 1, 1, 0]

이 코드는 다음과 같은 방식으로 동작합니다:

answer 리스트를 가격 리스트와 같은 크기로 초기화합니다.
인덱스를 저장할 stack을 초기화합니다.
각 가격에 대해 반복하며 스택을 관리합니다.
- 현재 가격이 스택의 마지막 인덱스의 가격보다 작으면, 해당 인덱스를 스택에서 제거하고 떨어지지 않은 기간을 계산하여 answer에 저장합니다.
- 현재 인덱스를 스택에 추가합니다.
반복이 끝난 후에도 스택에 남아 있는 인덱스는 끝까지 가격이 떨어지지 않은 경우이므로, 각 인덱스에 대해 떨어지지 않은 기간을 계산하여 answer에 저장합니다.

이 코드는 각 가격에 대해 한 번만 반복하여 시간 복잡도를 O(n)으로 유지합니다. 이를 통해 더 효율적으로 문제를 해결할 수 있습니다.

그래서 이 코드를 프로그래머스에 집어넣으면?

뭐지? 효율성 떨어지는데? 아까 내 deque코드랑 다를 바가 없잖아!!!! 이해가 안가네요.

그리고 분명히 FIFO FIRST IN FIRST OUT 이니까 큐 문제였던 것 같은데!!!
LIFO라고?????

stack과 deque의 차이

stack과 deque의 주요 차이는 LIFO와 FIFO 방식이라는 점입니다. 이를 좀 더 구체적으로 설명하면 다음과 같습니다:

Stack (스택):
- LIFO (Last In, First Out): 마지막에 들어온 항목이 가장 먼저 나가는 방식입니다.
- 일반적으로 list 자료형을 사용하여 구현하며, append 메서드로 항목을 추가하고 pop 메서드로 항목을 제거합니다.
- 예제:

stack = []
stack.append(1)  # 스택에 1 추가
stack.append(2)  # 스택에 2 추가
last_item = stack.pop()  # 스택에서 마지막 항목(2) 제거 및 반환

2. Deque (덱, Double-Ended Queue):

FIFO (First In, First Out): 먼저 들어온 항목이 먼저 나가는 방식입니다. 덱은 양쪽 끝에서 항목을 추가하거나 제거할 수 있어서 더 유연합니다.
collections 모듈의 deque 자료형을 사용하여 구현하며, append와 appendleft 메서드로 항목을 추가하고, pop과 popleft 메서드로 항목을 제거합니다.
예제:

from collections import deque
dq = deque()
dq.append(1)        # 덱의 오른쪽 끝에 1 추가
dq.appendleft(2)    # 덱의 왼쪽 끝에 2 추가
first_item = dq.popleft()  # 덱의 왼쪽 끝 항목(2) 제거 및 반환

스택과 덱의 차이점을 요약하면 다음과 같습니다:

스택:
- LIFO 방식
- 항목 추가: append
- 항목 제거: pop
덱:
- 양방향 큐 (양쪽 끝에서 항목 추가/제거 가능)
- 항목 추가: append, appendleft
- 항목 제거: pop, popleft

따라서, 스택은 주로 LIFO 방식으로 동작하는 자료구조이며, 덱은 FIFO 방식과 LIFO 방식을 모두 지원하는 유연한 자료구조입니다.

덱은 FIFO, LIFO 모두 지원하고 스택은 LIFO를 지원하는구나...이상하다...강사님 수업할 때 졸았나...잘못알고 있었구만. 그런데 뭐가 더 효율적이라는 거지? 니 코드도 for 문 안에 while문 들어있으니까 시간 복잡도 O(n^2) 아니야?

해당 코드는 겉보기에는 이중 반복문처럼 보이지만, 실제로는 선형 시간 복잡도 𝑂(𝑛)로 동작합니다. 이 점을 이해하기 위해서는 스택의 동작 방식을 고려해야 합니다.
코드의 작동 방식을 다시 한번 살펴보겠습니다:

def solution(prices):
    answer = [0] * len(prices)
    stack = []
    
    for i, price in enumerate(prices):
        # 스택이 비어 있지 않고 현재 가격이 스택의 마지막 가격보다 작으면
        while stack and price < prices[stack[-1]]:
            j = stack.pop()
            answer[j] = i - j
        stack.append(i)
    
    # 스택에 남아 있는 인덱스들에 대해 가격이 떨어지지 않았던 시간 계산
    while stack:
        j = stack.pop()
        answer[j] = len(prices) - 1 - j
    
    return answer

# 테스트
prices = [1, 2, 3, 2, 3]
print(solution(prices))  # 출력: [4, 3, 1, 1, 0]

여기서 중요한 점은 각 요소가 스택에 정확히 한 번 추가되고, 한 번 제거된다는 점입니다. 따라서, 스택 연산은 각 요소마다 한 번만 수행됩니다.

for 루프: 각 가격에 대해 한 번씩 반복합니다. 이 루프 자체는 𝑂(𝑛)입니다.
while 루프: 스택에서 요소를 제거하는 작업은 최대 𝑛번 수행됩니다. 각 요소는 스택에 한 번 추가되고 한 번 제거됩니다.

이중 반복문처럼 보이지만, 실제로는 다음과 같습니다:

각 요소는 스택에 한 번 추가되고 한 번 제거되므로, 스택 연산은 총 𝑂(𝑛)입니다.

이러한 이유로, 전체 시간 복잡도는 𝑂(𝑛)입니다. 스택을 이용한 방법은 효율적이며, 주어진 문제를 선형 시간 내에 해결할 수 있습니다.
따라서, 이 코드의 시간 복잡도는 𝑂(𝑛)입니다. 이는 주어진 문제에서 최적의 성능을 제공합니다.

무슨 말이지? 그니까 for문안의 while문은 단순 append pop하는기능만 수행한다는거지?

그럼 다시 코드를 살펴보겠습니다.

def solution(prices):
    answer = [0] * len(prices)
    stack = []#가격들의 위치, index정보를 담는다
    
    #가격이 떨어진 경우만 찾는다, answer에 가격이 떨어진 기간만큼 담는다.
    for i, price in enumerate(prices):
        
        if stack:#디버깅용
            stackend = stack[-1] #비교할 이전 가격의 index정보
            before = prices[stack[-1]]#위의 index정보를 넣어서 나온 가격
        
        # while stack 스택이 비어 있지 않고 and 현재 가격price가 price의 이전가격(들)보다 작으면 
        # stack의 마지막 값, 즉 이전가격을 빼주고 answer에 걸린 시간을 넣어준다. 
        # 즉, stack에는 prices에서 갑자기 하락하기 전의 값을 빼주는거다. 
        # 최종 stack에는 처음부터 끝까지 쭉 상승하는 값들만 남게된다.

        while stack and price < prices[stack[-1]]: #현재price < 이전price
            # 추가:이 문장에서 while stack이란 조건이 앞에 있지 않으면 stack[-1]은 에러가 난다
            j = stack.pop() # 다음 price가 지금 price보다 작은 경우 stack안에 있는 index값을 빼준다
            answer[j] = i - j #현재 인덱스 i와 가격이 떨어진 시점의 인덱스 j의 차이
        # 스택이 비어 있거나 현재 가격이 이전 가격보다 크거나 같으면
        stack.append(i)
    
    # 스택에 남아 있는 인덱스들, 즉 가격을 게속 유지한 인덱스들에 대해 시간을 계산하여 가격에 담음.
    while stack:
        j = stack.pop()
        answer[j] = len(prices) - 1 - j
    
    return answer

# 테스트
prices = [1, 2, 3, 2, 3]
print(solution(prices))  # 출력: [4, 3, 1, 1, 0]

뭔지 알 것 같은데 아무래도 stack에 index를 넣고 활용하는 문제를 좀 더 연구해 봐야 할 것 같습니다. GPT에게 이러한 문제를 알려달라고 했습니다.

Next Greater Elemnet 오른쪽에 위치한 큰 수 stack으로 문제풀기

인덱스를 스택에 넣어 활용하는 대표적인 문제로 "오큰수 (Next Greater Element)" 문제가 있습니다. 이 문제는 다음과 같습니다:

문제 설명

정수 배열 nums가 주어졌을 때, 각 원소에 대해 자신보다 오른쪽에 있는 첫 번째 큰 수를 찾는 문제입니다. 해당하는 큰 수가 없으면 -1을 반환합니다.

예제

입력: nums = [2, 1, 2, 4, 3]
- 출력: [4, 2, 4, -1, -1]
입력: nums = [1, 2, 3, 4, 5]
- 출력: [2, 3, 4, 5, -1]
입력: nums = [5, 4, 3, 2, 1]
- 출력: [-1, -1, -1, -1, -1]

해결 방법

스택을 이용하여 각 원소의 인덱스를 저장하면서 문제를 해결할 수 있습니다. 스택을 활용하면 시간 복잡도를 𝑂(𝑛)로 줄일 수 있습니다.

스택을 활용한 해결 방법

인덱스를 저장하기 위한 스택을 초기화합니다.
각 원소를 순회하면서 스택의 맨 위 원소가 현재 원소보다 작으면 스택에서 꺼내고, 그 인덱스에 대한 결과를 현재 원소로 설정합니다.
스택이 비거나 스택의 맨 위 원소가 현재 원소보다 크면 현재 원소의 인덱스를 스택에 추가합니다.
순회가 끝난 후에도 스택에 남아 있는 인덱스들은 자신보다 큰 원소가 없는 경우이므로, 이들에 대해 결과를 -1로 설정합니다.

코드

def nextGreaterElements(nums):
    n = len(nums)
    answer = [-1] * n
    stack = []  # 인덱스를 저장하는 스택

    for i in range(n):
        while stack and nums[stack[-1]] < nums[i]:
            j = stack.pop()
            answer[j] = nums[i]
        stack.append(i)
    
    return answer

# 테스트
nums = [2, 1, 2, 4, 3]
print(nextGreaterElements(nums))  # 출력: [4, 2, 4, -1, -1]

nums = [1, 2, 3, 4, 5]
print(nextGreaterElements(nums))  # 출력: [2, 3, 4, 5, -1]

nums = [5, 4, 3, 2, 1]
print(nextGreaterElements(nums))  # 출력: [-1, -1, -1, -1, -1]

코드 설명

초기화:
- answer 리스트를 -1로 초기화합니다. 이는 자신보다 큰 원소가 없는 경우의 기본 값을 나타냅니다.
- stack은 빈 리스트로 초기화하여 인덱스를 저장합니다.

n = len(nums)
answer = [-1] * n
stack = []

2. 배열 순회:

각 원소를 순회하면서 현재 원소가 스택의 맨 위 원소보다 큰 경우, 스택에서 인덱스를 꺼내고 해당 인덱스의 결과를 현재 원소로 설정합니다.

for i in range(n):
    while stack and nums[stack[-1]] < nums[i]:
        j = stack.pop()
        answer[j] = nums[i]
    stack.append(i)

3. 결과 반환:

모든 원소를 순회한 후 결과 리스트 answer를 반환합니다.

return answer

이 코드에서는 스택을 활용하여 각 원소의 인덱스를 저장하고, 오른쪽에 있는 첫 번째 큰 수를 효율적으로 찾을 수 있습니다. 이를 통해 문제를 𝑂(𝑛) 시간 복잡도로 해결할 수 있습니다.

이 문제는 그냥 이런 방식을 암기해야 하네요. 익숙해지니 deque방식말고 stack방식으로도 풀 수 있을 것 같습니다!

deque보다는 stack방식으로 풀라는 강사님의 말씀이 기억나네요. 시간복잡도 때문에 stack을 권하고 또 코테에서 stack이 더 많이 나온다고 합니다.

기타 문제

Next Greater Element 문제를 더 풀어봅시다.

백준: 오큰수: https://www.acmicpc.net/problem/17298

N=int(input())
A=list(map(int, input().split()))
stack=[]
answer=[-1]*N
for i in range(N):
    while stack and A[i]>A[stack[-1]]:
        j = stack.pop()
        answer[j] = A[i]
    stack.append(i)    
print(*answer)

이 문제는 그냥 암기해야 합니다. 다음은 릿코드 문제입니다.

릿코드: next-greater-element-i : https://leetcode.com/problems/next-greater-element-i/

이 문제는 for문을 두 번 도는 방법, O(n^2)인 경우와 hash, stack을 이용한 O(n)인 경우 2가지로 풀 수 있습니다.

1. for문을 두 번 도는 방법, O(n^2)인 경우

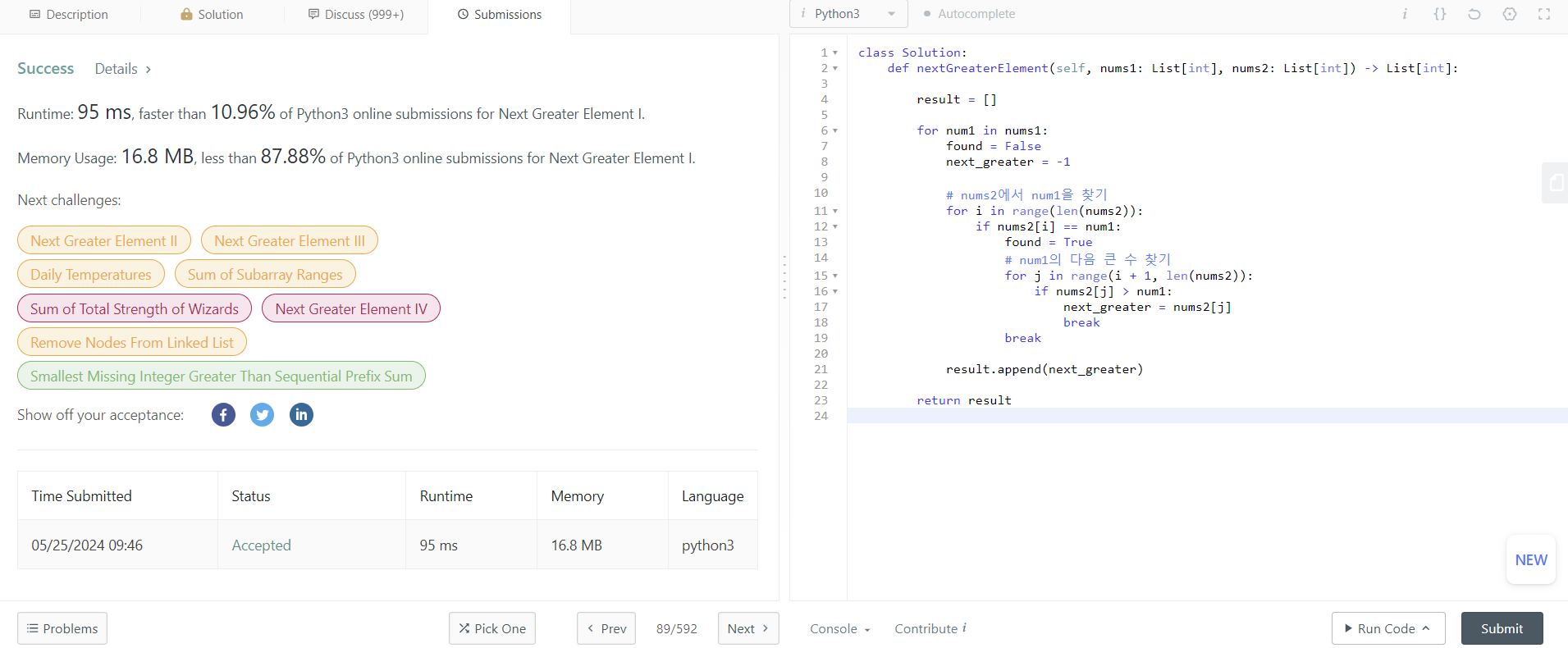
2. hash, stack을 이용한 O(n)인 경우

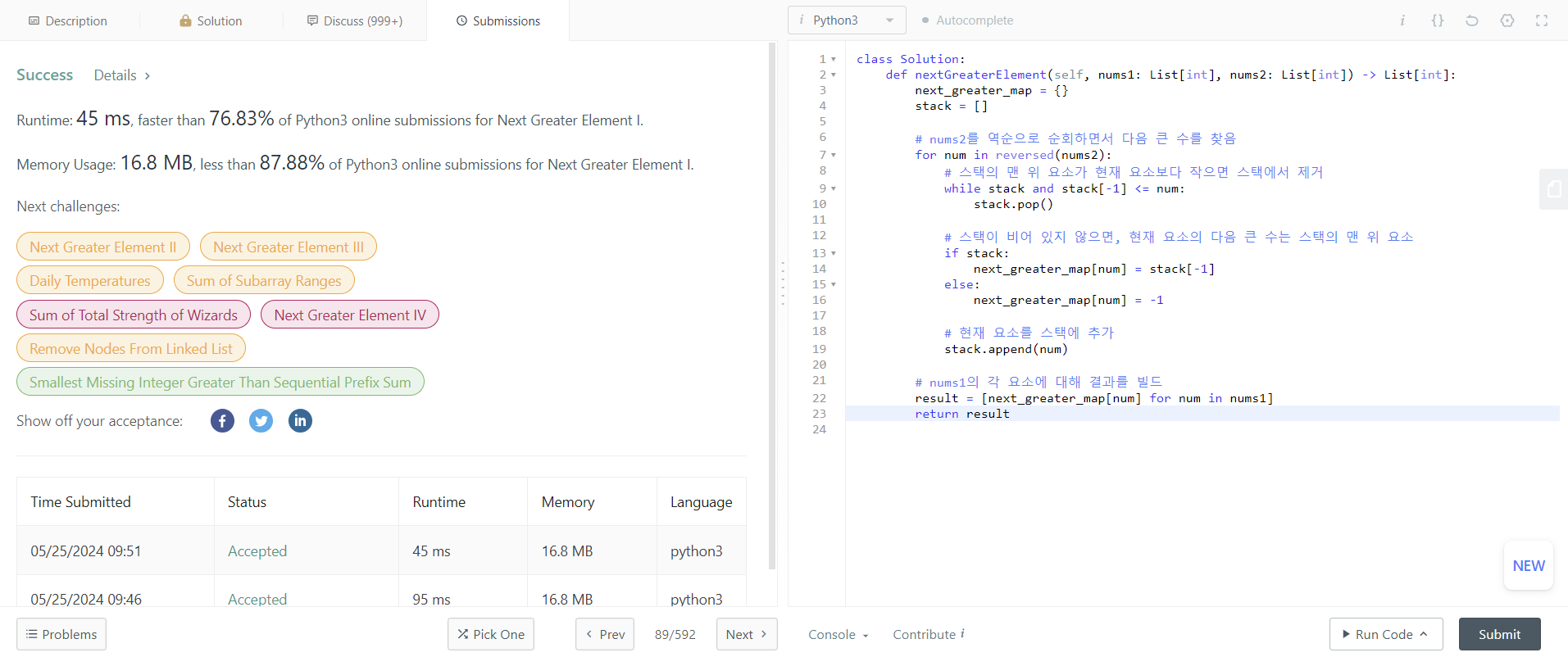
for문을 두 번 도는 경우보다 속도가 훨씬 빠릅니다. 해쉬를 배워야만 하는 문제이네요.

이제 해쉬를 배우러 떠나보겠습니다.

'코딩테스트' 카테고리의 다른 글

[파이썬] 해시맵 HashMap (0)	2024.05.26
[파이썬] TwoSum 해시로 풀기 (0)	2024.05.25
[파이썬] 스택/큐 > 기능개발 (0)	2024.05.23
코딩테스트 푸는 방법 코테 풀기 팁 (0)	2024.05.21
[파이썬] 스택/큐 > 다리를 지나는 트럭 (0)	2024.05.21

250x250

공지사항

최근에 올라온 글

최근에 달린 댓글

Total

Today

Yesterday

링크

TAG more

« 2024/12 »
일	월	화	수	목	금	토
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30	31

글 보관함

문과생CS정복기

Table of Contents