Table of Contents

p값을 이해하기 쉽게 설명하자면, 어떤 일이 우연히 일어날 가능성을 나타내는 숫자라고 할 수 있어요. 예를 들어서, 우리가 주사위를 던져서 6이 나오는 게 특별한 마법 때문인지, 그냥 우연인지 알아보고 싶을 때, p값을 사용할 수 있어요.
만약 주사위를 한 번 던져서 6이 나왔다면, 그것이 마법 때문이라고 확신하기는 어렵죠. 왜냐하면 주사위를 던지면 어차피 1부터 6까지 숫자 중 하나는 나오게 되어 있으니까요. 이 때의 p값은 "아, 이건 마법이 아니야, 그냥 우연이야"라고 말해주는 숫자라고 생각하면 돼요. p값이 크면 클수록, 그 일이 그냥 우연히 일어났다고 보는 거고, p값이 작으면 작을수록 그 일이 특별한 이유가 있을지도 모른다고 생각하는 거예요.
p-value(평범값)
= 그냥 우연히 일어날 가능성
= 특별한 일이 아닐 가능성
= 평범pyungbum할 가능성

p값을 이해할 때는, 그래프에서 p값이 끝쪽에 위치하는 것을 생각해 볼 수 있어요. 우리가 아이스크림을 쌓아 높이기 게임을 한다고 상상해 볼까요? 아이스크림을 쌓다 보면 보통은 일정 높이까지만 쌓을 수 있어요. 그런데 만약에 누군가가 정말 높이 아이스크림을 쌓았다면, 그건 특별한 기술이나 도구를 사용했을 가능성이 커요. 아이스크림이 높이 쌓인 것은 보통 일어나지 않는 일이니까요.
이 예에서 아이스크림을 평범한 높이까지 쌓는 것을 '귀무가설' null hypothesis 이라고 생각하면 돼요. 즉, 아무런 특별한 도구나 기술 없이 아이스크림을 쌓는 것이죠. 하지만 아이스크림이 예상보다 훨씬 높이 쌓였다면, 우리는 '대안가설'Alternative hypothesis,을 생각해볼 수 있어요. 즉, 누군가가 특별한 도구나 기술을 사용했다는 거죠.

'귀무가설' null hypothesis은 처음부터 버릴 것을 예상하는 가설이에요. 차이가 없거나 의미있는 차이가 없는 경우의 가설이에요. 이것이 맞거나 맞지 않다는 통계학적 증거를 통해 증명하려는 가설이지요.
귀무가설을 다음과 같이 정해봅시다.
"누구나 아이스크림 스쿱을 2개까지 쌓을 수 있다."
이건 너무 당연한걸까요? 하지만 어떤 사람들은 2개도 못 쌓을 수 있잖아요. 한 번 맞는 안맞는지 통계학적으로 증명해 보자구요.
여러 실험을 토대로 아이스크림 쌓은 개수를 통계분포로 그릴 수 있게 되었다고 합시다.
그런데 이게 왠일이죠?
사람들이 6개 이상 쌓은 경우가 99% 즉 p-value가 0.01이 나오게 된 것이죠.
이렇게 결과가 나오다니 제 (귀무)가설은 틀렸네요. 사람들이 2개까지 쌓을 평범할 가능성이 이렇게 작다니 다른 반대의 (대립,대안)가설Alternative hypothesis, 즉, "사람들은 3개 이상의 아이스크림을 쌓는다"를 채택해야 겠네요.

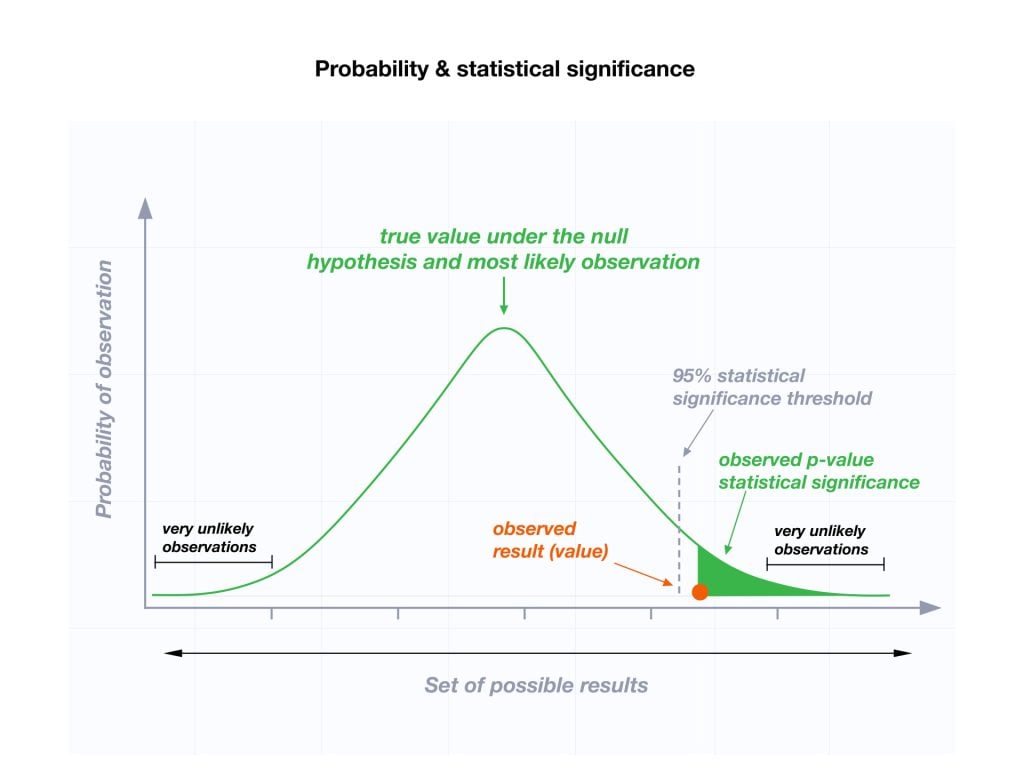
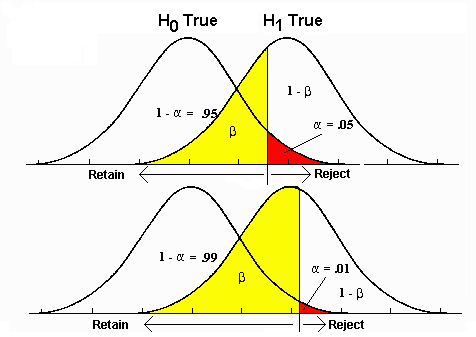
p값이 그래프 분포도 끝쪽에 위치하는 것은, 아이스크림이 예상치 못하게 높이 쌓인 것처럼, 어떤 일이 일어날 확률이 매우 낮다는 걸 보여줘요. p값이 작으면, 우리가 보고 있는 일이 우연히 일어났다고 보기 어렵다는 의미가 되고, 평범할 가능성이 작게 되요. 그래서 귀무가설을 기각하게 되요. 즉, 특별한 도구나 기술이 사용되었을 거라고 생각하는 거죠.

반면에 p값이 크다면, 그 일이 우연히 일어날 수 있는 일반적인 일이라고 생각하고, 평범할 가능성이 높게 되요. 즉, 귀무가설을 채택하게 돼요. 이렇게 해서 우리는 일이 우연인지 아니면 특별한 이유가 있는지를 판단할 수 있어요.
그렇다면 p-value는 어떤 값을 기준으로 판단하게 되는 걸까요?
p-value는 보통 0.05 0.01 0.001을 기준으로 판단해요 이건 지금까지 통계학 학문을 쌓아오신 분들의 경험을 토대로 만들어진 관습같은 거에요
그래서 단순히 pvalue가 0.05이니까 좋다고 말할 수 있는게 아니라 학문의 분야마다 다를 수 있고 논문의 특색에 따라 달라질 수 있어요

실제 가설을 세우고 검증을 진행해 봅시다.
ex 1)
'A 온라인 쇼핑몰'에서 상품 상세페이지 내 Buy 버튼의 위치를 두고 A/B Test를 진행합니다.
여기서 A는 기존에 사용하고 있던 상품 상세페이지이고, B는 Buy 버튼의 위치를 변경한 상품 상세 페이지입니다.
이때 귀무가설, 대립가설은 아래와 같습니다.
귀무가설: A와 B는 유의미한 차이가 없다.
대립가설: A와 B는 유의미한 차이가 있다.
만약, A/B test를 진행했는데 p-value =0.03 이 나왔다면 이는 낮은 pvalue이기 때문에 귀무가설을 기각하게 됩니다. 즉, 대립가설을 채택하게 되지요.

다른 예를 살펴봅시다.
ex 2)
제약회사에사 복제약을 만들었습니다. 원래 브랜드 약품의 효과를 비교합니다.
귀무가설 (H0): 복제약의 효과는 원래 브랜드 약품의 효과와 같다.
- 이는 통계적으로 "복제약과 원래 약품 간에 유의미한 차이가 없다"는 것을 의미해요.
대립가설 (H1): 복제약의 효과는 원래 브랜드 약품의 효과와 다르다.
- 이 가설은 복제약이 브랜드 약품보다 더 나은 효과를 낼 수도 있고, 더 못할 수도 있음을 포함하여, 어떠한 차이도 유의미하다고 보는 것이죠.
이런 설정은 약품의 효과를 과학적으로 검증하기 위해 매우 중요해요. 연구 결과에 따라 귀무가설이 기각되면, 복제약과 원래 약품 간에 통계적으로 유의미한 차이가 있다고 결론지을 수 있어요. 반면, 귀무가설을 기각하지 못하면 복제약과 원래 약품이 같은 효과를 갖는다고 볼 수 있겠죠. 이런 과정을 통해 복제약의 유효성과 안정성을 과학적으로 평가할 수 있어요.

이제 pvalue가 이해되었나요?
'통계' 카테고리의 다른 글
| t-test t검정/ ANOVA 분산분석 (0) | 2024.04.25 |
|---|---|
| 종속표본 t-test t검정 (0) | 2024.04.25 |
| 독립표본 / 종속표본 / t-test t검정/ t-stat t통계량/ p-value유의확률/ two-tailed test양측검정 (0) | 2024.04.25 |
| 산술평균 기하평균 조화평균 (0) | 2024.04.24 |
| 귀무가설/ 대립가설/ 1종 오류/ 2종 오류/ 유의확률p-value (0) | 2024.04.24 |
- Total
- Today
- Yesterday
- PEFT
- Python
- Lora
- nlp
- 파이썬
- 오블완
- Array
- classification
- cnn
- clustering
- Github
- LIST
- RAG
- t5
- LLM
- #패스트캠퍼스 #패스트캠퍼스AI부트캠프 #업스테이지패스트캠퍼스 #UpstageAILab#국비지원 #패스트캠퍼스업스테이지에이아이랩#패스트캠퍼스업스테이지부트캠프
- 손실함수
- 코딩테스트
- 해시
- 리스트
- Transformer
- #패스트캠퍼스 #패스트캠퍼스ai부트캠프 #업스테이지패스트캠퍼스 #upstageailab#국비지원 #패스트캠퍼스업스테이지에이아이랩#패스트캠퍼스업스테이지부트캠프
- recursion #재귀 #자료구조 # 알고리즘
- speaking
- #패스트캠퍼스 #UpstageAILab #Upstage #부트캠프 #AI #데이터분석 #데이터사이언스 #무료교육 #국비지원 #국비지원취업 #데이터분석취업 등
- 티스토리챌린지
- Hugging Face
- git
- Numpy
- English
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |

